Jak vypočítat obsah výseče mezikruží?

Obsah výseče mezikruží se vypočítá podle vzorce S = (α / 360°) · π · (R² − r²), kde α je středový úhel, R vnější a r vnitřní poloměr.

Jak zjistit délku oblouku výseče mezikruží?

Délky oblouků se vypočítají podle vztahů l₁ = (α / 360°) · 2πR a l₂ = (α / 360°) · 2πr.

Jak se liší výseč mezikruží od výseče kruhu?

Výseč mezikruží je oblast mezi dvěma soustřednými výsečemi o stejném středovém úhlu, zatímco výseč kruhu má pouze jeden poloměr.

Jaký je obvod výseče mezikruží?

Obvod výseče mezikruží se počítá jako O = l₁ + l₂ + 2(R − r), tedy součet obou oblouků a dvou poloměrů.

V jakých jednotkách se udává středový úhel?

Středový úhel lze udávat ve stupních (°) nebo v radiánech. Při výpočtech je nutné jednotku zachovat konzistentně.

VÝSEČ MEZIKRUŽÍ

VÝSEČ MEZIKRUŽÍ:

VÝPOČET POLOMĚRŮ, ÚHLU, OBVODU A OBSAHU VÝSEČE MEZIKRUŽÍ ZE VZTAHŮ:

Pozor!

Zrejme mate vypnutou podporu JavaScriptu.

V tomto pripade vypocet nebude funkcní!!!

Geometrické znázornění výseče mezikruží s vyznačenými poloměry a průměry a středovým úhlem,

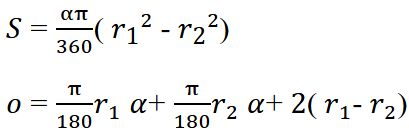Vzorce pro ovbod a obsah výseče mezikruží

TIP: pokud máte zadanou jinou veličinu k výpočtu výseče mezikruží můžete ji dopočítat ze vztahů pro kruh nebo kruhového oblouku

Zadejte jakékoliv tři veličiny a zvolte všechny jednotky

VÝSLEDKY

Poloměr kružnice r₁ =
Poloměr kružnice r₂ =
Uhel α =		°
obvod výseče o =
Obsah výseče S =

r₁
r₂
α		°
o
S

pozn.: výsledné hodnoty jsou zaokrouhlovány na tři desetinná místa

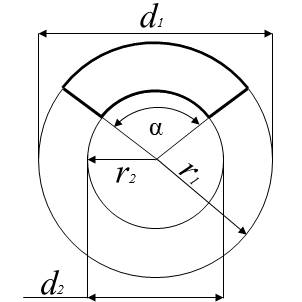
Definice výseče mezikruží

Výseč mezikruží (nebo také prstencová výseč) je část mezikruží ohraničená dvěma soustřednými oblouky a dvěma poloměry svírajícími středový úhel α.

Je tvořena částí mezikruží odpovídající úhlu α.
Ohraničena je dvěma kruhovými oblouky (vnitřním a vnějším) a dvěma poloměry.
Při úhlu α = 360° tvoří celé mezikruží.

Tento tvar se často využívá při výpočtech částí prstencových konstrukcí nebo ploch v technické praxi.

Obsah výseče mezikruží

Obsah výseče mezikruží (S_v) je část obsahu mezikruží odpovídající úhlu α.

pro úhel ve stupních: S_v = (π · (r₁² − r₂²) · α) / 360°
pro úhel v radiánech: S_v = ((r₁² − r₂²) · α) / 2

Tento vztah vyjadřuje, že výseč mezikruží zaujímá část plochy celého mezikruží úměrnou úhlu α.

Obvod výseče mezikruží

Obvod výseče mezikruží (o_v) je tvořen dvěma oblouky a dvěma poloměry.

o_v = l₁ + l₂ + 2 · (r₁ − r₂)

Kde:

l₁ = (πr₁α) / 180° – délka vnějšího oblouku (ve stupních)
l₂ = (πr₂α) / 180° – délka vnitřního oblouku (ve stupních)

Při úhlu v radiánech platí: l₁ = r₁α a l₂ = r₂α, tedy o_v = (r₁ + r₂)α + 2(r₁ − r₂).

Délka oblouků výseče mezikruží

Výseč mezikruží má dva soustředné oblouky – vnější a vnitřní.

vnější oblouk: l₁ = (πr₁α) / 180° nebo l₁ = r₁α
vnitřní oblouk: l₂ = (πr₂α) / 180° nebo l₂ = r₂α

Délky oblouků jsou přímo úměrné poloměrům a středovému úhlu α.

Zajímavosti o výseči mezikruží

Výseč mezikruží je častým tvarem v mechanice a strojírenství (např. v rotujících částech).
Při úhlu α = 360° tvoří celé mezikruží, při α = 180° jeho polovinu.
Slouží jako model pro výpočty plošných momentů setrvačnosti prstencových plátů.
Objevuje se i v architektuře – např. jako segment prstencových kleneb.
Při zanedbatelném rozdílu mezi r₁ a r₂ se výseč mezikruží blíží kruhové výseči.