Jak vypočítat obsah kruhové úseče?

Obsah kruhové úseče se vypočítá podle vzorce S_u = S_v − (1/2) · r² · sin(α), kde S_v je obsah výseče a α středový úhel.

Jak zjistit výšku kruhové úseče?

Výšku kruhové úseče lze spočítat ze vztahu v = r − √(r² − (t² / 4)), kde t je délka tětivy.

Jaký je vztah mezi výsečí a úsečí?

Výseč je část kruhu vymezená dvěma poloměry a obloukem, zatímco úseč je část kruhu vymezená obloukem a tětivou. Obsah úseče je vždy menší než odpovídající výseč.

Jak se počítá tětiva z poloměru a úhlu?

Délku tětivy lze spočítat vzorcem t = 2r · sin(α / 2).

Jak se určí délka oblouku úseče?

Délka oblouku úseče je úměrná středovému úhlu a vypočítá se jako l = (α / 360°) × 2πr.

KRUHOVÁ ÚSEČ

KRUHOVÁ ÚSEČ:

VÝPOČET OBVODU, OBSAHU, POLOMĚRU, ÚHLU, DÉLKY OBLOUKU, VÝŠKY OBLOKU A DÉLKY TĚTIVY KRUHOVÉ ÚSEČE ZE VZTAHŮ:

Pozor!

Zrejme mate vypnutou podporu JavaScriptu.

V tomto pripade vypocet nebude funkcní!!!

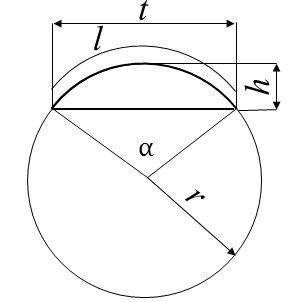TIP: pokud máte zadanou jinou veličinu k výpočtu mezikruží můžete ji dopočítat ze vztahů pro kruh

Zadejte jakékoliv dvě veličiny a zvolte všechny jednotky

VÝSLEDKY

Poloměr kružnice r =
Uhel α =	°
Délka oblouku l =
Výška oblouku h =
Délka tětivy t =
Obvod kruhové úseče o =
Obsah kruhové úseče S =		²

r
α		°
l
h
t
o
S

pozn.: výsledné hodnoty jsou zaokrouhlovány na tři desetinná místa

Definice kruhové úseče

Kruhová úseč je část kruhu ohraničená obloukem kružnice a tětivou spojující jeho krajní body. Vzniká tedy jako „odříznutá“ část kruhu pod obloukem.

Je určena poloměrem r a středovým úhlem α, nebo výškou v.
Při úhlu α = 180° tvoří polokruh.
Menší část se nazývá menší úseč, větší větší úseč.

Kruhové úseče se často používají při návrhu obloukových konstrukcí, výpočtech ploch i v inženýrské geometrii.

Obsah kruhové úseče

Obsah kruhové úseče (S_u) se určí jako rozdíl mezi obsahem kruhové výseče a trojúhelníkem o stranách tvořených poloměry a tětivou.

S_u = S_v − S_t

Po dosazení dostaneme vztah:

pro úhel v radiánech: S_u = (r² / 2) · (α − sin α)
pro úhel ve stupních: S_u = (πr²α / 360°) − (r² · sin α / 2)

Tento vzorec se využívá při přesných plochových výpočtech, např. v technických výkresech a strojírenství.

Obvod kruhové úseče

Obvod kruhové úseče (o_u) je součet délky oblouku a tětivy, která úseč uzavírá.

o_u = l + t

Kde:

l = r · α – délka oblouku (při úhlu v radiánech)
l = (πrα) / 180° – délka oblouku (při úhlu ve stupních)
t = 2r · sin(α / 2) – délka tětivy

Obvod kruhové úseče tedy vyjádříme jako:

o_u = rα + 2r · sin(α / 2)

Tento vztah se používá například při určování délky obloukových hran nebo rozvinutí zakřivených tvarů.

Délka tětivy kruhové úseče

Tětiva (t) spojuje krajní body oblouku a vymezuje základnu kruhové úseče.

Podle středového úhlu: t = 2r · sin(α / 2)
Podle výšky úseče: t = 2√(2rv − v²)

Tětiva se zkracuje s menším úhlem α nebo menší výškou úseče.

Výška kruhové úseče

Výška kruhové úseče (v) je vzdálenost mezi tětivou a nejvzdálenějším bodem oblouku.

Lze ji vypočítat:

z poloměru a tětivy: v = r − √(r² − (t² / 4))
nebo z úhlu: v = r · (1 − cos(α / 2))

Výška úseče roste s úhlem α; při 180° je rovna poloměru kruhu.

Délka tětivy kruhové úseče

Tětiva (t) je přímka spojující koncové body kruhového oblouku.

Lze ji vypočítat pomocí středového úhlu nebo výšky oblouku:

Podle úhlu: t = 2r · sin(α / 2)
Podle výšky: t = 2√(2rv − v²)

Délka tětivy roste s velikostí úhlu α – při 180° je tětiva rovna průměru kruhu.

Středový úhel kruhové úseče

Středový úhel (α) je úhel, který svírají dva poloměry spojující střed kruhu se dvěma krajními body oblouku.

Lze ho vypočítat ze známé délky oblouku:

v radiánech: α = l / r
ve stupních: α = (l · 360°) / (2πr)

Zajímavosti o kruhové úseči

Kruhová úseč je základní tvar pro obloukové stropy, mosty a potrubní průřezy.
V technické praxi se používá k výpočtu objemů válcových nádrží naplněných částečně kapalinou.
Při úhlu 180° tvoří přesně polokruh.
Je úzce spjata s kruhovým obloukem – má stejnou tětivu a středový úhel.
Její výpočet kombinuje poznatky z trigonometrie, geometrie i fyziky.