TROJÚHLENÍK OBECNÝ
TROJÚHLENÍK OBECNÝ:
VÝPOČET OBSAHU, OBVODU, STRAN, ÚHLŮ, VÝŠKY OBECNÉHO TROJÚHELNÍKU A POLOMĚRU KRUŽNIC TROJŮHELNÍKU VEPSANÉ A OPSANÉ ZE VZTAHŮ:
 |
 |
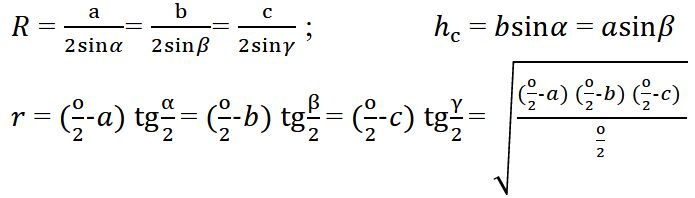 |
|
TROJÚHLENÍK OBECNÝ
 |
 |
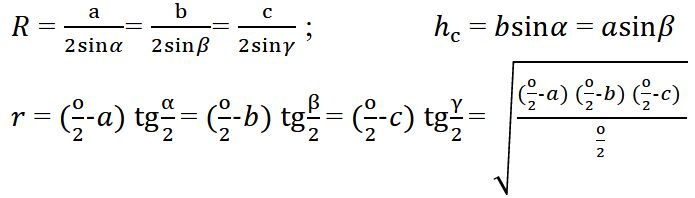 |
|
Definice obecného trojúhelníku
Definice obecného trojúhelníku
Obecný trojúhelník je rovinný geometrický útvar, který má tři strany, tři vrcholy a tři vnitřní úhly.
Základními prvky jsou strany a, b a c a úhly α, β, γ, které jsou jim protilehlé.
Obvod trojúhelníku
Obvod trojúhelníku
Obvod (O) trojúhelníku se vypočítá jako součet délek všech jeho stran:
O = a + b + c
Tento vztah platí pro každý trojúhelník bez ohledu na jeho typ.
Obsah trojúhelníku
Obsah trojúhelníku
Obsah (S) trojúhelníku lze určit několika způsoby podle známých údajů:
Heronův vzorec je univerzální a lze jej použít, pokud známe délky všech tří stran.
Výška trojúhelníku
Výška trojúhelníku
Výška trojúhelníku (va) je kolmá vzdálenost vrcholu od protilehlé strany. Lze ji vyjádřit vztahem:
va = (2S) / a
Každý trojúhelník má tři výšky, které se protínají v jednom bodě nazývaném ortocentrum.
Poloměr kružnice vepsané trojúhelníku
Poloměr kružnice vepsané trojúhelníku
Poloměr kružnice vepsané (rv) udává vzdálenost středu vepsané kružnice od stran trojúhelníku. Vypočítá se podle vzorce:
rv = S / s
Kružnice se dotýká všech tří stran trojúhelníku a její střed se nazývá incentrum.
Poloměr kružnice opsané trojúhelníku
Poloměr kružnice opsané trojúhelníku
Poloměr kružnice opsané (ro) je vzdálenost středu kružnice od vrcholů trojúhelníku. Vypočítá se podle vztahu:
ro = (a · b · c) / (4S)
Kružnice opsaná prochází všemi třemi vrcholy a její střed se nazývá circumcentrum.
Zajímavosti o trojúhelníku
Zajímavosti o trojúhelníku