LICHOBĚŽNÍK
LICHOBĚŽNÍK:
VÝPOČET OBSAHU, OBVODU, STRAN, ÚHLŮ, VÝŠKY, ÚHLOPŘÍČEK A STŘEDNÍ PŘÍČKY LICHOBĚŽNÍKU ZE VZTAHŮ:
 |
 |
 |
|
 |
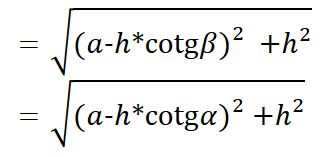 |
LICHOBĚŽNÍK
 |
 |
 |
|
 |
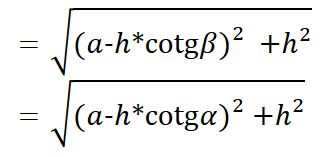 |
Definice lichoběžníku
Definice lichoběžníku
Lichoběžník je rovinný geometrický útvar patřící mezi čtyřúhelníky, který má:
Rozlišujeme několik druhů lichoběžníků:
Obsah lichoběžníku
Obsah lichoběžníku
Obsah lichoběžníku (S) se počítá podle vzorce:
S = ((a + c) / 2) · v
kde a a c jsou délky základen a v je výška lichoběžníku. Tento vzorec vychází z průměru délek základen násobeného výškou.
Jinak řečeno: lichoběžník má stejný obsah jako obdélník, jehož délka odpovídá střední příčce a výška je stejná jako výška lichoběžníku.
Obvod lichoběžníku
Obvod lichoběžníku
Obvod (O) se vypočítá jednoduše součtem délek všech čtyř stran:
O = a + b + c + d
kde a a c jsou základny a b, d jsou ramena lichoběžníku.
Střední příčka lichoběžníku
Střední příčka lichoběžníku
Střední příčka lichoběžníku je úsečka, která spojuje středy jeho ramen. Je rovnoběžná se základnami a její délka se určí podle vzorce:
m = (a + c) / 2
Střední příčka má tedy délku rovnou aritmetickému průměru délek obou základen. Lze si ji představit jako „průměrnou základnu“ lichoběžníku.
Výška lichoběžníku
Výška lichoběžníku
Výška (v) lichoběžníku je kolmá vzdálenost mezi jeho základnami.
Pokud známe obsah a délky základen, lze ji dopočítat ze vzorce:
v = (2S) / (a + c)
Výšku lze sestrojit pomocí kolmice vedené z vrcholu jedné základny na druhou.
Úhlopříčky lichoběžníku
Úhlopříčky lichoběžníku
Obecně mají lichoběžníky dvě úhlopříčky, které se různě protínají, ale nejsou stejně dlouhé (kromě rovnoramenného lichoběžníku).
Jejich délky lze určit pomocí rozšířeného kosinova zákona, například:
d₁ = √(a² + b² - 2ab·cos(β))
d₂ = √(c² + d² - 2cd·cos(δ))
U rovnoramenného lichoběžníku jsou úhlopříčky shodné a protínají se v ose souměrnosti.
Zajímavosti o lichoběžníku
Zajímavosti o lichoběžníku